Integration for Idiots, Part II: Background and Background Subtraction
Series by Ali and TBV
In Part I, we saw how selection of the left-right integration limits affects the computed and reported results of a peak with a known value.
Having looked at left and right, let's look at up and down.
Up is defined by the top of the peaks in question, so there is nothing to be done there. But down at the bottom, unlike the clean theoretical examples in Part I, there is in reality background noise, and we need to decide what to do about it.
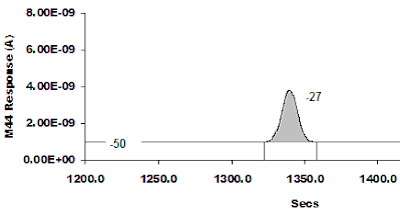Figure 6: Illustrates the addition of background noise to the peak. The background has been given a true o/oo of -50 (similar to that present during Floyds analysis). With good background removal, the measured value is -27. The true value for this peak is -27.
Figure 7: Illustrates the effect of incomplete background removal. The residual background in the peak results in a measurement of -30.9. The true value for this peak is -27.
Figure 8: Illustrates the effect of no background removal. The residual background in the peak results in a measurement of -38.6. The true value for this peak is -27.
Figure 9: Illustrates the addition of sloping background noise to the peak. The background has been given a true o/oo of -50 (similar to that present during Floyds analysis). With good background removal, the measured value is -27. The true value for this peak is -27.
Figure 10: Illustrates the effect of incomplete background removal. The residual background in the peak results in a measurement of -30.2. The true value for this peak is -27.Therefore, we see clearly that decisions made for background subtraction have significant effects on the computed results, and that sloping backgrounds complicate matters making the background subtraction more difficult to select.
These complications are true in the simplest, clearest possible examples with peaks having known values.
In Part III, we'll look at the confusing effects of neighboring peaks.
2 comments:
TBV and Ali -
I think you guys are trying to point out some theoretical problems in terms of determining the areas of peaks. But I'm losing the feel of the problem we're trying to address in real world terms.
1. In part one of your Idiots course, it was clear we were talking about IRMS graphs, because that's where you see the problem with overlapping peaks. In parts II and III, are we now talking about issues that can affect both GC/MS and IRMS peaks? I think so, but you've moved from part I to part II without saying that we're looking at more than one kind of graph now.
2. I would think that in theory, the problem in part II is the same as the problem in part I, which is that we have to correctly identify where a peak begins and ends. Presumably, if you know where your peak begins, you've solved the background subtraction problem, because the point at the very beginning of the peak has a y-axis value of zero. Or am I missing something?
3. If you assume a flat line level of background noise, as in Figure 6, again in theory I don't see a problem. As you trace the curve of the peak from left to right, there's going to be some point where the curve loses its slope, where the line you're tracing is parallel to the x-axis. You could then define the peak as ending at that point, assign that point a y-axis value of 0, and you're half-way home. You could reverse these directions and find where the peak begins. Maybe it's harder to do this than it sounds, but I don't see how anyone can make the errors you're showing in Figures 7 and 8. Of course, we're dealing with a flat background in these figures, but you're not making it seem like it's difficult to deal with a flat background of noise.
4. OK, Figure 9 is more challenging to deal with than the earlier figures. But again, this doesn't look so hard, as the background you've drawn is a straight line on a particular slope. So, instead of using the method I described in paragraph 3 above where you find points on the peak where the slope of the peak is parallel to the x-axis, in Figure 9 you find the points on the peak where the curve is parallel to the background noise line. And again, you assign those points a y-axis value of zero. In theory, this doesn't seem any harder than any of the other examples.
5. Where things get tough, I imagine, is where you're dealing with an irregular pattern of background noise, and it's not clear what kind of noise line the peak is perched upon. Luckily, with the GC/MS and IRMS charts I'm used to seeing, no single peak covers too wide an expanse of the x-axis, so there's not all that much room under any given peak for wild variations in the noise level. But you guys have not talked about irregular noise levels, so I won't discuss this question any further.
In any event, this problem looks much easier to resolve than the problem you presented in lesson 1, and the errors you're showing in background removal look much easier to avoid than the errors you showed in lesson 1. Am I missing something?
Good questions, Larry.
1. These are all IRMS. The main issue we are talking about is the computed carbon isotope ratio. While the issues have different manifestations in the GCMS, they are more critical to the CIR.
Yes, mathematically they are all similar problems, but this is the idiots course, and we're showing each effect separately. If we were smart enough to get the gestalt instantly from the equations, we'd have understood Herr Doktor Professor's slides without needing these idealizations.
2. "If you know where the peak begins" is very much the point; in the real world you don't. It definately never approaches zero, because of the background.
3. If you have a uniform, non-noisy background, yes, you are much more likely to get good results. It's particularly easy with well separated peaks, or as they say in the jargon, "baseline separated peaks".
4. If you really know the slope, and it isn't changing, and there aren't other issues, yes, you can deal with it. It's later when you are compounding issues and don't know what the truth is that it becomes difficult to say what is going on.
5. I think you haven't seen any clean chromatograms to know what a clean baseline looks like. You're used to seeing the LNDD results.
What you're missing is touched on in Part III, where I'm about to get to your next comment.
TBV
Post a Comment