Integration for Idiots, part I: limits
Integration for Idiots
Part I: Exploring integration limits
Series by Ali and TBV.
Part I: Exploring integration limits
Series by Ali and TBV.
Integration is the process by which we get the carbon isotope ratios out of the IRMS peaks. The sample gets burned up into carbon dioxide, ionized, and detectors for the m=44 and m=45 ions determine how many of carbon 12 molecules vs. the number of carbon 13 molecules there are.
Because they are of slightly different mass, the heavier 13 comes through a before the 12, by a little bit, so the resulting peak is not completely symmetrical, but carries a lopsidedness dependent on the ratio of the carbons. As a result, you need to be careful where you start and stop counting molecules for determining the ration.
This is explained for smart people in the Meier-Augenstein paper starting in GDC 1101 at GDC 1107. It has this picture showing the offset:
To explore integration, we've created a spreadsheet to make the following simplified examples that illustrate the issues. The spreadsheet is in the archive here, and you're invited to use it to play with values yourself, and to find any errors we've made in it.
Starting off with a well separated and perfectly formed peak, the following series of examples illustrates the sensitivity of the o/oo value to integration limits, background noise and interfering peaks. In part I, we're going to show the effects of changing left and right integration limits on the computed isotope (o/oo) ratio.
Figure 1: A normal peak with no interference from adjacent peaks. The true o/oo value is -27 and the measured value (indicated on the graph) is also -27.
Figure 2: The effect of moving the left hand integration limit in. The measured value is now -28.9. The true value for this peak is still -27.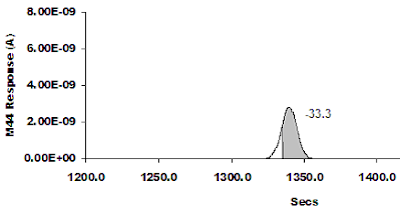
Figure 3: Keep moving the left hand integration limit further in, and the computed value is now -33.3. The true value for this peak is still -27.
Figure 4: The effect of moving the right hand integration limit in. The measured value is now -25.7. The true value for this peak is still -27.
Figure 5: Keep moving the right hand integration limit in and the measured value is now -22.2. The true value for this peak is still -27.In showing this, we are not saying or suggesting anybody or anything is doing anything wrong of this sort in the tests. The automatic selection of limits has the same set of issues. We're just showing the kinds of effect changing the limits does have on computed results.
Next in Part II, background and background subtraction.
12 comments:
OK, I think I need the 101 course that's the prerequisite for the idiot's course!
Let me see if I have this figured out. I'll make a series of statements and you can tell me if I'm right or wrong.
1. The problem we're facing here is that we need to separately figure out the area of two different curves on the IRMS charts. One curve is the C13 curve and the other is the C12 curve. It's the ratio of the area under the C13 curve to the area under the C12 curve that gives us one of the values in the delta-delta calculation that gets used to determine whether an athlete is doping with exogenous testosterone.
2. The "integration" problem has to do with the fact that the two curves overlap. The C13 curve is the earlier curve and the C12 is the later curve. Because the curves overlap, you can't see on the chart where the C12 curve begins or where the C13 curve ends. And you can't compute the area of either curve without knowing (or guessing) where each curve begins and ends.
3. The "left hand integration limit" is our guess where the C12 curve begins. If we guess wrong and place the curve beginning too far to the right, we underestimate the area of the C12 curve and we boost the C13/C12 ratio above its real limit.
4. The "right hand integration limit" is our guess where the C13 curve ends. If we guess wrong and place this end too far to the left, we underestimate the area of the C13 curve and we shrink the C13/C12 ratio below its real limit.
OK, Professors, did I pass or do I have to retake remedial mass spectroscopy?
By the way, it appears from your spreadsheet that integration errors lead to changes in peak time. If this is true, can you also accurately state this in reverse: that if a peak has an unexpected peak time (i.e., it's earlier or later than you'd expect on the basis of relative retention times), this could be caused by an integration error?
Remember, we're dealing with the simplest possible case, a single, theoretically perfect peak.
1. Essentially correct, though as soon as we hit the real world things get more complicated.
2. In the real world, you don't know where the curves really begin and end because it's messy. The best you can do is approximate and live with a n amount of uncertainty that you need to understand. You aren't completely guessing either, but the trick is that there may not be a correct solution.
3 and 4: yup.
Changes in peak time? Can you provide an example? We don't think that is supposed to happen, and we're not sure what you think you're seeing.
In an instrument, the method of identyfying a peak center is algorithmic, and might be affected by placement of manual integration limits. More typical would be assignment of peak identities first, then setting of integration points. A center selection might use something like: find the highest point, then look on either side for 1/2 that height, and say the peak is 1/2 way between those locations (full width, half max).
So unless you truncate the region being searched with an integration limit, the identity of the peak center shouldn't move around.
The spreadsheet doesn't do peak identification at all; it generates known data at the place you set. Early versions of the spreadsheet used the number as the peak start instead of the center, and there may be some vestiges of that causing confusion. If it's broke, we'll fix it.
TBV
TBV, on integration and peak times, I'm probably just failing to understand the spreadsheet. I just noticed that there were three peak times in row 7. I thought that these were three different scenarios for setting three different integration limits for the same peak; on closer look I see that they're decribing the actual peak times for the three peaks in the first graph.
If you move an integration limit, I suppose you might slightly change a peak time, but not by very much. Certainly not by the 6% - 7% described by Dr. M-A.
Anyway, I'm just pleased I was close to the mark in my paragraphs 1-4.
I need the course for "pre-idiots".
str
This is what I needed back in Calculus class as a real world example for our plotting the area under the curve!
Moving the left time limit shifts the "value" from -27 to -33.3
Moving the right time limit shifts the value from -27 to -22.2
But the true value hasn't changed at all.
Keep the lessons coming.
Dang, and all that with just ten numbers and 26 letters! I'm just overwhelmed.
str and others, the explanation here is a lot like what Mark Twain used to say about the music of Richard Wagner: "it's not as bad as it sounds."
The integration issue is a very simple one, I think. It's the SOLUTIONS to the issue that are going to get complicated.
(TBV and Ali, correct me if I'm wrong ...)
"Integration" is the problem of dealing with an IRMS graph that has two curves on it, like the first picture shown in the TBV-Ali article. The curves are drawn one on top of the other, with one curve slightly to the right of the other. But unlike the picture in the TBV-Ali article, on the IRMS graph you can't see the shape of each curve; you can only see the outer outline of the combined curves. You can see where the first curve begins but not where it ends; you can see where the second curve ends but not where it begins.
To figure out if the athlete failed the doping test, you have to know the shape of each curve individually. That requires you to know where BOTH curves begin and end (among other things). When TBV and Ali describe moving "integration limits" to the right and left, what they're doing (more or less) is trying to figure out where the first curve ends and the second curve begins.
I think this is going to get a lot more complicated before TBV and Ali are finished, but so far it's not so bad.
larry,
The instantaneous 45/44 plot (second from top) provides a good indication of when the m45 (C13) peak starts and when the m44 (C12) peak ends. Integration should be performed over this entire period for accurate results. However, once you get peaks close together, with additional content between them, determining the true start and stop times from the 45/44 plot can be problematic as the true shapes can become distorted. This can lead to invalid selection of integration limits.
Incidentally, as the spreadsheet is set up, the default C13 to C12 time shift is 100 ms. This is conservative and biases the results toward being less negative than they might otherwise be with a more typical value of 150 ms. The resolution is in steps of 0.1 s, so it can't accept 0.15 s. It can be changed to 0.2 s though (cell C9).
If you're happy enough with the concepts above, then it won't get any more complicated. What we're looking at is how these effects can be invoked unknowingly (and possibly systematically) due to factors such as poor peak seperation or unwanted interference.
This is a great tutorial.
I am curious what happens if the m=45 plot is adjusted (shifted) later in time so that the interval of integration for the m=44 and m=45 plots becomes the same. I suspect that the 45/44 plot becomes something approximating a rectangular pulse for a substance with good separation. Irregularities in the shape of the rectangle would suggest problems with the isolation of the target substance.
The appropriate time shift for the m=45 plot should be available from analysis of the peaks in the calibration samples. You could shift the m=45 plot so that the center of gravity of its peaks aligns with the center of gravity of the m=44 peaks. Or, you could shift the m=45 plot later in time until recangular pulses resulted in the ratio plot.
I think that the width and shape of the m=45 and m=44 peaks would be determined by the GC column before combustion. The width should be the same. The shapes should be the same, but scaled to different heights, reflecting the isotopic ratio.
I think that the difference in arrival time for the m=45 and m=44 peaks would be a consequence of different rates of progress after the combustion chamber, not while the carbon is part of more complicated molecules in the GC column. The difference in arrival time for the m=45 and m=44 peaks would be the same for all of the GC peaks.
In principle, once the correction is made for the slower progress of the ligher carbon after combustion, the isotopic ratio should not vary across the peak. The shift in time should transform the S-shaped ratio curve into a rectangular pulse. To the extent that the isotopic ratio does vary, it suggests a problem with the measurement.
I don't have any way to determine whether this is a valid test for the integrity of the isotope ratio measurement, but it seems like an interesting test to apply. It is such a simple test.
TBV and Ali,
The processs that I propose above can be visualized using the spreadsheet that you provided.
Enter a "C13-C12 times" of 0. This is equivalent to shifting the m=45 plot data later in time to compensate for the faster passage through the post-combustion column. As a consequence, the "Peak 1" "error o/oo" goes from -4.63 to -0.40. And, the "45/44 Ratio" plot becomes 3 merged but distinguishable peaks, not S-shaped curves.
Then, modify the "C12 Background" "start level" by multiplying it by 0.00001. (The spreadsheet appears to not handle correctly a value of 0 in this cell, so instead I just make it very small.) This is equivalent to correctly eliminating the background contribution to the isotopic ratio. At this point, the "45/44 Ratio" plot has two rectangular peaks merged with a rounded peak between them, due to the contribution of "Peak 3". The interference of "Peak 3" is obvious. And, it would be more accurate to integrate across just the portion of the peak without the interference. (This is only the case after the time shift above.)
I don't know whether this approach is valid for a real data set, but it sure looks good with the spreadsheet.
I was hoping that Davis would do something like this when he had the opportunity to do the data processing demonstration during the hearing, but it didn't turn out that way. Of course, the data set was only turned over just before the hearing. Maybe something more interesting will be done for the appeal.
I realize these observations are outside the themes of the tutorial and so I am just posting these comments where the spreadsheet was introduced.
Hugh,
The data set has never been turned over. The demonstration was done with data as relevant as the stuff in the tutorial.
By the way, I didn't go back to look, but when you originally ran into the left peak affects right peak issue, did you work any of this through? It seems to be a physical property, and not an artifact of the calculation as was thought by some at the time.
thx,
TBV
TBV,
The earlier arrival of the heavier isotope is a real physical effect, but I am suggesting a different way to analyze the data.
All of the literature and discussions look at integrating across a broad enough interval so that all of the carbon generated by a substance is part of the integration. If the integration can occur across all of the carbon without interference, the measurement can be accurate. But, getting rid of the interference is a problem.
I am suggesting that the m=45 and m=44 plots might be aligned so that it is meaningful to look at the ratio of the isotopes across a portion of the full interval. This should work if the distribution of the heavier isotope is uniform acros the duration of the peak in the GC column, with the faster progress of the heavier isotope only occurring after the combustion. (That may be a big "if".) Without the alignment, you would be comparing the amount of C12 to the amount of C13 that was in the GC column about 100ms later when you look at only a portion of the peak.
Without interference, this time-shift approach is likely less accurate. With interference, it might be more accurate. And, it will give some indication of the variation in isotopic ratio across the peak, which will likely provide some indication of the degree of interference.
It there an electronic data set available that includes both calibration and sample data?
I certainly got the impression that the defense team received the data set a couple of weeks before the hearing, but that Suh said that was insufficient time to analyze it. This was at the end of the cross of the first lab tech.
Post a Comment